There is a problem named N Queens which is famous in computer science courses and some programming challenges. Most of the websites who claim to explain the solution are either copying the solution from other place or memorizing it. They don’t fully understand or solve the problem themselves. So, I started trying the problem myself and developed an iterative solution as workaround and converted it into a recursive solution.
The problem statement can be found here:
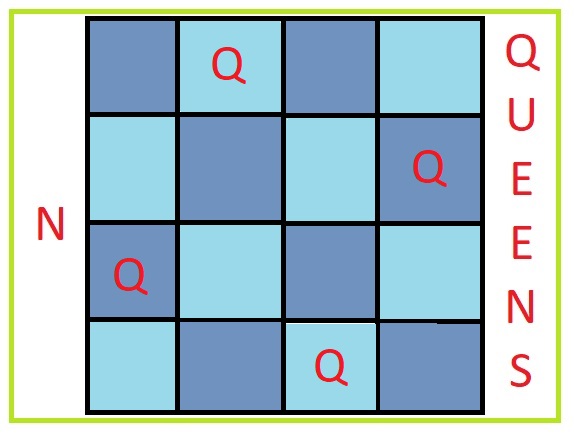
As on learning about the problem we can understand that in NxN chessboard we have to place N queens in such a way that no queen can capture another queen. For problem to be simple and computable, max N range is proposed to be very low that is 10.
Simplest solution possible
In place of going through recursion which is difficult to understand, let’s try another approach. We will then derive recursive solution through this approach.
Our method is generate all possibilities of placing N queens in the NxN board and then check if queen don’t attack each other. For generating all possible placings we can run N nested loop and place queen at one position in each loop. Let’s try with the smallest possible queens that is 4.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
class RecurQueens{
static final int max=30;
static Integer board[][]=new Integer[max][max];
static int numQ=4;
// as we need to print the fist board only
static boolean boardPrinted=false;
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//Taking number of N for NxN board and N queens from console.
numQ = Integer.parseInt(br.readLine());
initializeBoard();
recursePlaceQueensAtXRow(0);
if(boardPrinted == false){
System.out.println("Not possible");
}
}
static boolean isValidBoard(int n){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
//current cell has value 1 so queen is present in it
if(board[i][j]==1)
{
/*As we are already clearing row before new queen
placement in the row we don't need to write logic for
checking multiple queens on same row */
/* logic to check multiple queen on same column */
for(int c=i-1;c>=0;c--){
if(board[c][j]==1){
return false;
}
}
/* logic to check queen on left diagonal path '\' .*/
for(int c=i-1,r=j-1;c>=0 && r>=0;c--,r--){
if(board[c][r]==1){
return false;
}
}
/* logic to check queen on right diagonal path '/' .*/
for(int c=i-1,r=j+1;c>=0 && r<max;c--,r++){
if(board[c][r]==1){
return false;
}
}
}
}
}
return true;
}
/*As we can place only one queen in a row,
on setting new queen in same row,
we need to remove/reset other queen in that row.*/
static void clearBelowRows(int n){
for(int j=n;j<max;j++){
for(int i=0;i<max;i++){
board[j][i]=0;
}
}
}
/* Initializing board is setting 0 value at every row and column
so setting all rows values to 0 */
static void initializeBoard(){
clearBelowRows(0);
}
static void printBoard()
{
for(int i=0;i<numQ;i++){
for(int j=0;j<numQ;j++){
System.out.print(board[i][j]);
if(j<numQ-1){
System.out.print(" ");
}
}
if(i<numQ-1){
System.out.println();
}
}
System.out.println();
}
/*Generate all possibilities for placing 4 queen in 4 rows columns.*/
static void placeQueens(int n){
for(int a=0;a<n;a++){
clearBelowRows(0);
board[0][a]=1;
for(int b=0;b<n;b++){
clearBelowRows(1);
board[1][b]=1;
for(int c=0;c<n;c++){
clearBelowRows(2);
board[2][c]=1;
for(int d=0;d<n;d++){
clearBelowRows(3);
board[3][d]=1;
printBoard();
}
}
}
}
}
/*as we see loops containing a, b, c and d variables
are same loops running on different rows of the board,
to reduce complexity of code we use the recursive function,
by deriving it from above iterative code.*/
//The equivalent recursive code
static void recursePlaceQueensAtXRow(int x){
//don't continue computing if board already printed
if(boardPrinted == false){
for(int a=0;a<numQ;a++){
//clear all queens before placing another on row
clearBelowRows(x);
//place the queen on (value of 'a') column of row
board[x][a]=1;
/*Check if current board is valid*/
if(isValidBoard(numQ)){
/* if n queens are not placed on n rows
then call function again with new row to be filled */
if(x<numQ){
recursePlaceQueensAtXRow(x+1);
/* check if we have place numQ Queens */
if(x==numQ-1){
/*check if board is not printed once*/
if(boardPrinted==false ){
//print the board and set boardPrinted true
printBoard();
boardPrinted = true;
}
}
}
}
}
}
}
}
I have derived the recursive function from 4×4 iterative function. If you see both function you will find the similarity between both. This way we can derive the recursive function intuitively. In place of sending board from one recursive call to other I place it in shared space and by resetting the values using clearBelowRows() , I am able to reduce the space complexity of the code to… In this case the same code can be utilized for higher values of N for N-Queens problem. Only time complexity will not allow us to go beyond certain limit of values like 26 etc.