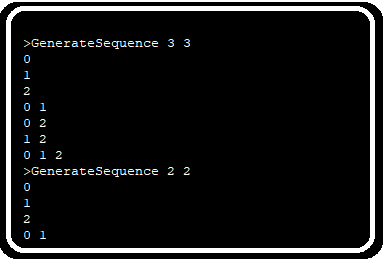
Recently during a “Hiring Hackathon” of a company I went through a problem which required, to get all the combination of an array element. That is if the array length is 3 then the combination of array index should look like below:
0
1
2
0 1
0 2
1 2
0 1 2
Let’s write code for the above output. In the very first attempt I thought to solve the problem for very small number like below
// Online Java Compiler
// Use this editor to write, compile and run your Java code online
class GenerateCombination {
public static void main(String[] args) {
int n=3;
int r=3;
for(int i=1;i<=r;i++){
generateCombination(3,i);
}
}
static void generateCombination(int n, int r){
if(r==1){
for(int i=0;i<n;i++){
System.out.println(i+ " ");
}
}
if(r==2){
for(int i=0;i<n;i++){
for(int j=i;j<n;j++){
if(i!=j)
System.out.println(i+" "+j+" ");
}
}
}
if(r==3){
for(int i=0;i<n;i++){
for(int j=i;j<n;j++){
for(int k=j;k<n;k++){
if(i!=j && i!=k && k!=j)
System.out.println(i+" "+j+" "+k+" ");
}
}
}
}
}
}
There is a problem with above code. It is that with every increase in value of r one need to write loop within loop for r times which isn’t possible as the code can not be written or modified for increasing value of r.
This solution can be converted into a recursive solution. So lets try to convert the above one into recursive solution. Lets say are recursive function is recurGenCombination then it must take n and r as integer or long values
void recurGenCombination(int n, int r){
}
Let’s store the printed value as a string within the function which can be passed in next recursive calls and increase:
void recurGenCombination(String currentCombination,int n, int r){
}
And to store the value of current level of combination lenght like 1 lenght or 2 length we take another variable:
void recurGenCombination(String currentCombination,int n, int r, int currentIter){
}
When we see our first attempt of looping we see we need to go through every value from 1 to n at each Iteration so there should be a loop in this function from 1 to n, and that value must be concatenated in our final string
void recurGenCombination(String currentCombination,int n, int r, int currentIter){
System.out.println(currentCombination);
currentCombination+=currentIter+" ";
while(currentIter<n){
currentIter++;
}
}
The above code will make the sequence for r=1 only, so in case of generating value for r=2 etc we need to call this function within itself.
static void recurGenCombination(String currentCombination,int n, int r, int currentIter){
if(currentIter>n+1){
return;
}
System.out.println(currentCombination);
currentCombination+=currentIter+" ";
while(currentIter<n){
currentIter++;
recurGenCombination(currentCombination,n,r,currentIter);
}
}
The function generate sequences for any particular n and r value of nCr :
So to generate all sequences we must call them in a loop:
class GenerateCombination {
public static void main(String[] args) {
int n=3;
int r=3;
for(int i=0;i<n;i++){
recurGenCombination("",n,r,i);
}
}
static void recurGenCombination(String currentCombination,int n, int r, int currentIter){
if(currentIter>n+1){
return;
}
if(currentCombination.length()>0){
System.out.println(currentCombination);
}
currentCombination+=currentIter+" ";
while(currentIter<n){
currentIter++;
recurGenCombination(currentCombination,n,r,currentIter);
}
}
}
The above code returns following result:
0
0 1
0 1 2
0 1
0
0 2
0
1
1 2
1
2
One drawback of the above function is that it generates some of the sequence multiple times. This happens because same function gets called for different values of currentIter variable, which print the sequence multiple time. In order to solve this issue, we can save the string value in Set, so that we get unique sequence.
We will have a global HashSet and in place of printing values we save values in HashSet:
import java.util.HashSet;
class GenerateCombination {
static HashSet<String> combinations=new HashSet<String>();
public static void main(String[] args) {
int n=3;
int r=3;
for(int i=0;i<n;i++){
recurGenCombination("",n,r,i);
}
System.out.println(combinations);
}
static void recurGenCombination(String currentCombination,int n, int r, int currentIter){
if(currentIter>n+1){
return;
}
if(currentCombination.length()>0){
combinations.add(currentCombination);
}
currentCombination+=currentIter+" ";
while(currentIter<n){
currentIter++;
recurGenCombination(currentCombination,n,r,currentIter);
}
}
}
This will return us the unique combination of r values from n total values and n >= r. The values look like below on running above code:
[0 , 0 2 , 0 1 , 1 2 , 2 , 0 1 2 , 1 ]
Conclusion
I wrote the above blog because, I tried a step by step approach to convert a simple intuitive solution into a recursive solution. With some combination and try, I could make the logic perfect and working for all values of n and r. I think this might be helpful in finding other intuitive solution to different problems which can be solved through recursion.