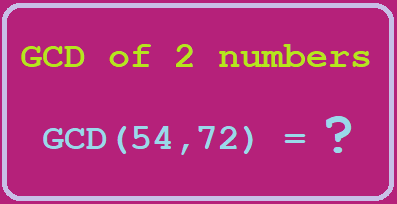Finding greatest common divisor of a number is a very common mathematics problem and has a lot of implementation in computer science like cryptography, data security and other fields. By definition GCD of two numbers is the largest number which can divide both numbers.
So, we can derive a naive algorithm based on the definition:
class GCD{
public static void main(String args[]){
System.out.println(gcd(10,20));
}
static int gcd(int a, int b){
int min=a;
if(b<a){
min=b;
}
for(int i=min;i>1;i--){
if(a%i ==0 && b%i==0)
return i;
}
return 1;
}
}
For large numbers which have very small GCD this algorithm go very very slow and test each and every number till GCD found. In such case to optimize the solution another approach of Euclidean method can be followed. According to this approach:
if a and b are two numbers for which we need to find GCD:
- Divide the bigger number from the smaller number
- Check if the remainder is 0 then the smaller number is the GCD
- if remainder is not 0 then divide smaller number from remainder and check step 2 again.
With above approach we can easily reduce the steps to find the GCD of two numbers.
class GCD{
public static void main(String args[]){
System.out.println(gcd(10,20));
}
static int gcd(int a, int b){
int remainder = -1;
int min=a;
int max=b;
if(b<a){
min=b;
max=a;
}
remainder = max%min;
if (remainder == 0)
return min;
else
return gcd(min, remainder);
}
}
Converting the algorithm to work for big integer we can do following:
import java.math.BigInteger;
class GCD{
public static void main(String args[]){
System.out.println(gcd(new BigInteger("15"),new BigInteger("20")));
}
static BigInteger gcd(BigInteger a, BigInteger b){
BigInteger remainder = new BigInteger("-1");
BigInteger min=a;
BigInteger max=b;
if(b.compareTo(a)<0){
min=b;
max=a;
}
remainder = max.mod(min);
if (remainder.compareTo(new BigInteger("0")) == 0)
return min;
else
return gcd(min, remainder);
}
}